Pokémon GO has taken the world by storm. Since its release on July 6, the augmented reality app has caught the attention of millions around the globe, with 23 million daily active users in the U.S. alone.
With the aim to "Catch 'Em All," Pokémon GO users spend an average of 43 minutes per day on the game (as of July 8). Just as in the original games, some Pokémon are rarer than others - and may take a bit longer to catch or evolve to in order to complete your Pokédex.
Is it really easier to evolve a Pokémon than find the rarer later stage? Or are your chances better out hunting instead of collecting candy?
Thanks to PokéAssitant and Serebii.net for data and Reddit user aem323 for inspiration for a cumulative probability formula, I was able to calculate the probability of catching or evolving to each of the 151 Pokémon.
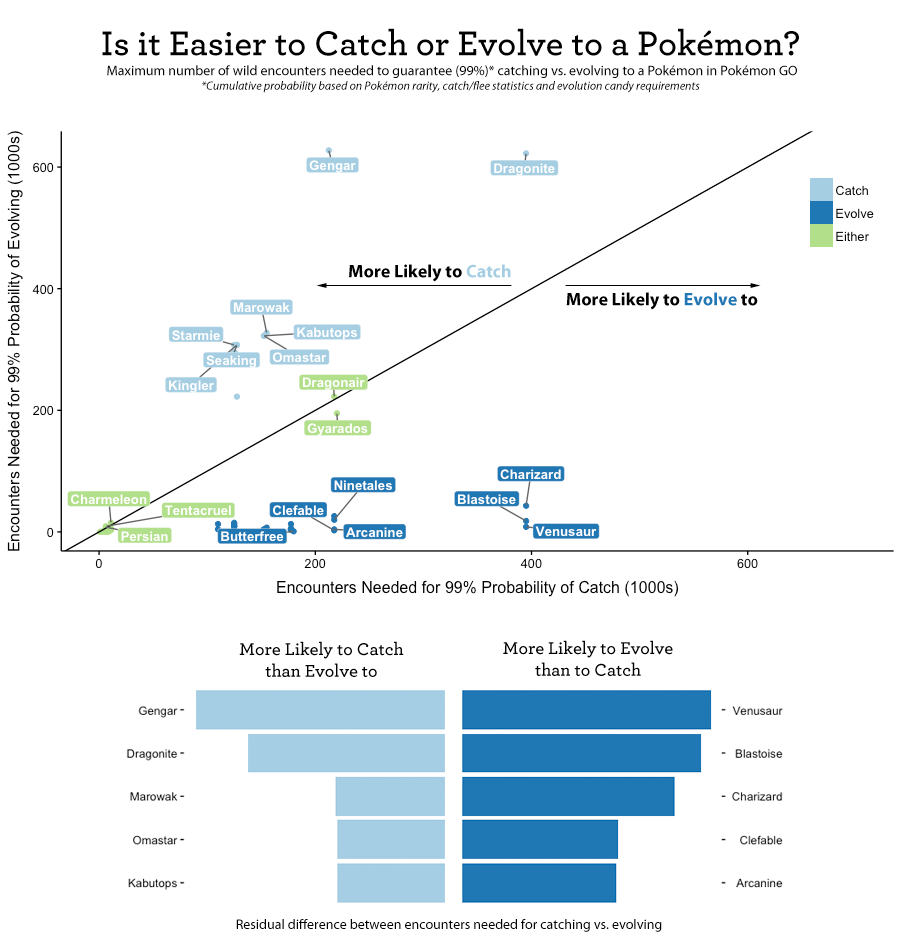
The chart above compares the total number of wild encounters needed to guarantee a catch or evolution to a Pokémon using cumulative binomial probability.1,2,3 This uses the chance of catching the Pokémon on any given wild encounter and the probability of catching lower-stage Pokémon to get enough candies to evolve.
That means that it could take almost 400,000 total wild Pokémon encounters to find and catch a Venusaur, but you could evolve to one in a fraction of the time.
Catch Probability: 1 Encounter
There are many factors that go into catching a Pokémon: your location and special items like Ultraballs or razz berries, and statistics like its rarity and its base catch and flee rates. For this analysis, only the base statistics were used.
The chart below shows the probability1 of catching a certain Pokémon (within 5 throws) on any one wild encounter.
[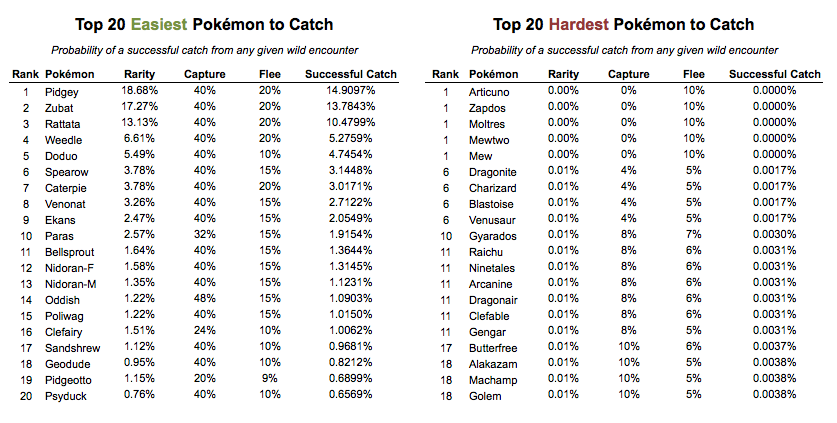
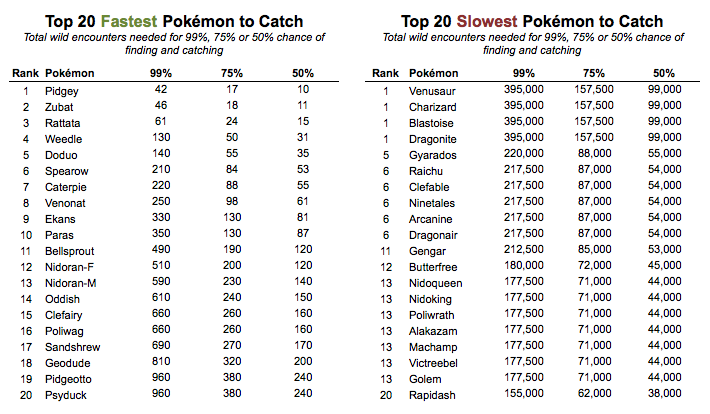
Pidgey is the most common and easiest Pokémon to find and catch, which supports the Pidgey-churning strategy some users employ to gain XP.
All of the top 20 easiest Pokémon to catch are first stage Pokémon, while all of the top 20 hardest to catch are final stage Pokémon (either they have no evolutions or have reached their final form).
The legendary birds Articuno, Zapdos and Moltres (which may be impossible to catch and instead special giveaways), along with Mew and Mewtwo top the list of most difficult Pokémon to catch. No catches have been reported yet.
Catch Probability: Over N Encounters
If your chances of finding and catching a Golem are only 0.0038% on any given encounter, how many encounters should it take you to finally get one?
I looked at the cumulative (binomial) probability2 and found how many wild encounters it could take to guarantee (99%) that you fill that spot in your Pokédex.
Since this takes rarity into account, this is total wild encounters needed - not just encounters with the Pokémon in question. It surely won't take you 42 Pidgey sightings to catch one - but it could take you up to 42 total Pokémon sightings to find and catch one.
Evolution Probability: Over N Encounters
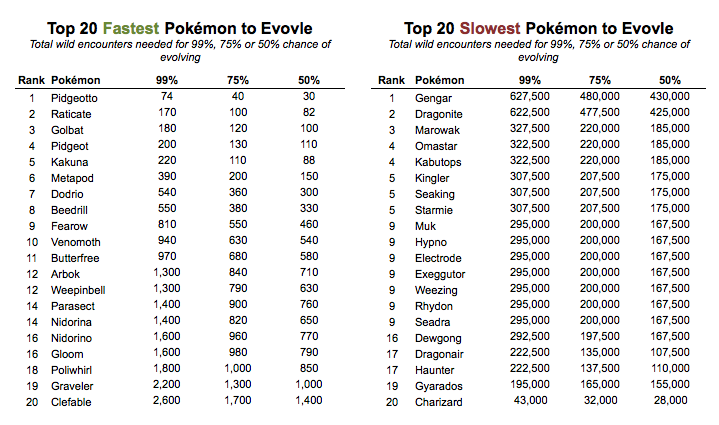
The probability for evolving to a Pokémon depends on a few things: how many candies are needed and the probability of catching the number of Pokémon you need with those candies.
For example, you need 12 Pidgey candies to evolve into Pidgeotto, so you need to catch 4 Pidgeys (3 candies each = 9 + 3 trades = 12, evolve the 4th). How many wild encounters would it take to reach 99% probability of catching 4 of them?
The answer is 74: it could take 74 wild Pokémon encounters to find and catch 4 Pidgeys. Depending on how long you play the game each day and how often you encounter Pokémon, this might take you one day or 3 weeks.
Finding a Charizard could take 395,000 encounters, but evolving to one could be done in 43,000 - so don't give up on those Charmanders.
Overall, there's no hard and fast rule for evolving vs. catching higher stage Pokémon. Some are easier to find and catch, while some are easier to evolve to.
Footnotes
-
The probability of a successful catch occurring at any given wild Pokémon encounter is calculated as $Success = Rarity * Catch.Probability$; where rarity is the reported incidence of that Pokémon in the game and ( Catch.Probability = \sum_{N=1}^5 [(1- \sum P) * (1-F)^{N-1} * P ] ); Catch probability is the chance that you'll come across the particular Pokémon and be able to successfully capture it within 5 throws. $P$ is base capture probability, $F$ is the base flee probability, $N$ is the throw number, and $1-\sum P$ is the probability of no successes on the previous throws.
-
The cumulative probability of finding and catching a Pokémon is: $\binom{n}{k}p^k(1-p)^{n-k}$ where $p$ = $Success$ of catching the Pokémon, $k$ = 1 and the number of trials ($n$) varied until certain probabilities (99%, 75% and 50%) were hit. The R function pbinom was used for these calculations.
-
The probability of evolution is the same as the formula used for catching the Pokémon, but $k = Candy/4 + 1$ (assuming the user trades each Pokémon for the additional candy) and $p$ = $Success$ of catching the base candy Pokémon rather than the Pokémon in question (catching Weedles for Weedle candy to get to Beedrill, e.g.).
All code and data can be found in my Github repo.